今天這題題目是國外論壇分享的面試題，
其實也是LeetCode-Path Sum的衍生題，直接來刷題吧！

簡單複習一下二元樹 Binary Tree 的特點：

1. 可以為空
2. 0 ≤ Node's Degree ≤ 2
3. 子樹有左右方向之區分

還記得Day 19：二元樹遍歷 Binary Tree Traversal我們提到的三種追蹤方式嗎？
今天我們會用到
前序追蹤（preOrder） “中左右”的方式還解決這題問題！

假設以下是我們一開始的樹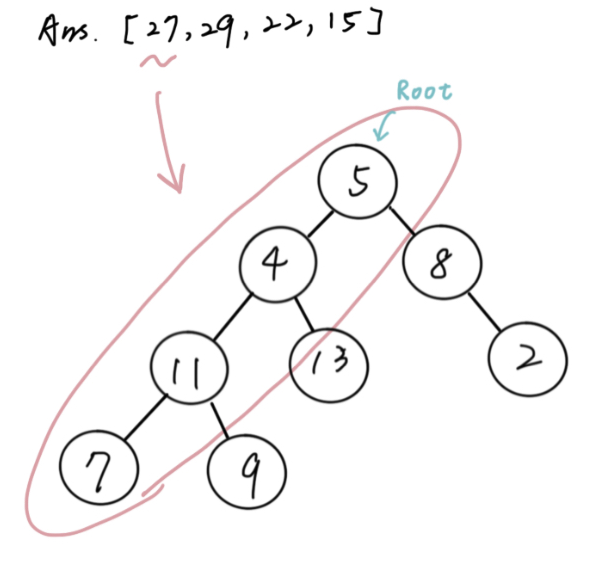

先思考一下，如果我們要獲得這棵樹的所有樹枝的加總，我們應該要怎麼做？
我們應該要拜訪每一個節點（node）對吧？
那要用哪一種方式呢？depth-first-search-like？

我們拜訪每一個節點的時候去把每個拜訪過的節點的值加起來。
我們知道，在二元樹的結構中，是有左右之分的，也就是每個節點都有可能有左右兒子。
這種重複性的結構我們應該想到用遞迴的方式。

沒錯我們其實就只用建立一個遞迴方法，把我們目前計算的結果存到array依序往左右兒子傳遞，直到左右兒子已經沒有後代就停止計算。

就像下面這張圖
在一開始初始化sum = 0
如第一次的答案 → 粉紅色１的路徑開始往下把拜訪過的數加總到sum，
走訪的路徑像是

5 → 哇５的左手牽著4 → 還沒完唷 4 的左手還拉著11 → 11左手又有 7 → 確定左邊沒了 → 回去11 發現右手還有9 在把暫存的+9 → 9沒有左右手了 → 退回4 ....這樣的走訪路徑

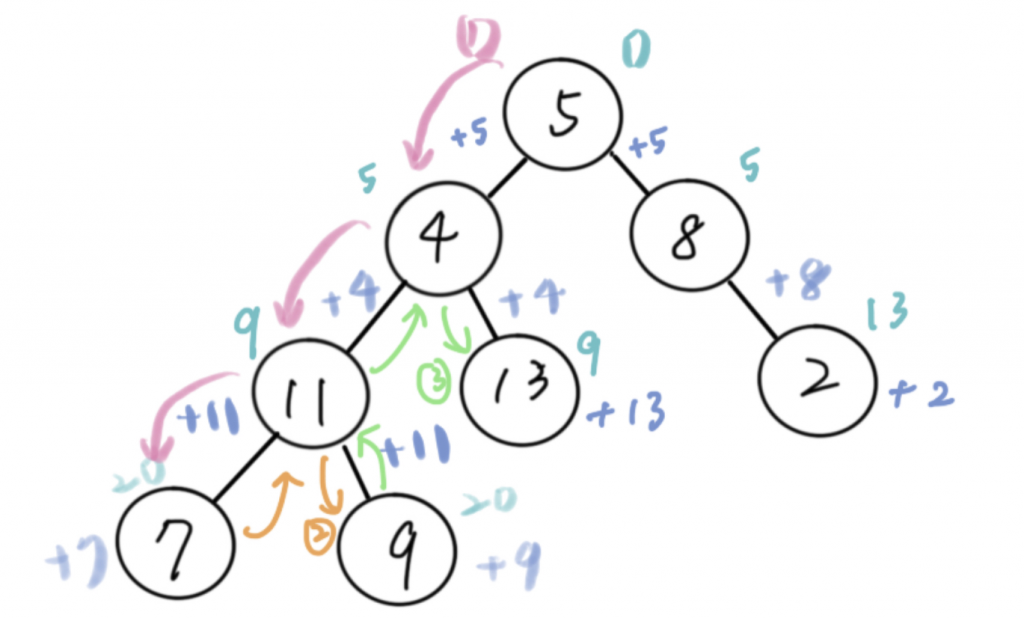
時間複雜度: O(n) 因為我們需要走訪每個node 沒個動作也只需要簡單的加總
空間複雜度: O(n) 為什麼呢？我們可以簡單說因為我們不可能獲得超過n的branch

我們來深入了解一下為什麼？
在範例中我們可以觀察到，答案的數量應該會跟完全沒有左右小孩的節點一樣多，在樹中我們叫做葉子(leaf)。
這張圖我們可以觀察到：當二元樹每一層都長滿的時候，下一層的節點數都恰好會是上一層的兩倍。
而所有的節點樹恰好就是 2^n層 -1
而最後一層的節點樹會是 2^ n-1
我們每次用來儲存結果的list大概就是為後一層的節點樹，也就是 2^ (n-1)
而節點的總數N = 2^n -1
所以 2^ (n-1) = (N+1) / 2
如果 N 趨近無限大時，我們可以說，最後一層的節點樹就會大約是一半的總節點樹。

可以參考下面來思考看看！

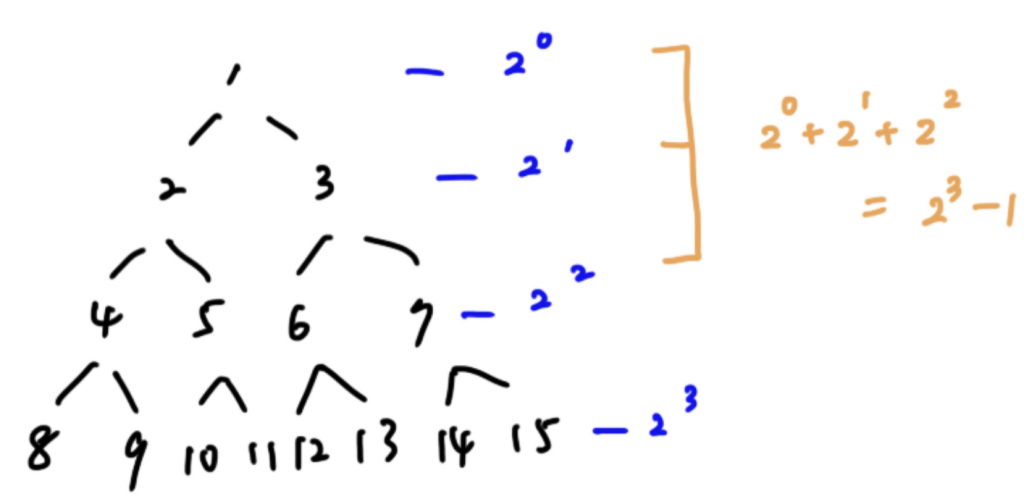
那我們來實作吧！

class BinaryTree {
  constructor(value) {
    this.value = value;
    this.left = null;
    this.right = null;
  }
}

function branchSums(root) {
  const sum = [];
  getBranchSums(root, 0, sum);
  return sum;
}

//遞迴function
function getBranchSums(node, tmpSum, sum) {
  //一開始檢查是否為節點 不是就停止遞迴呼叫
  if (!node) return;
  const currentSum = tmpSum + node.value;
  //如果左右都沒有節點了 答案放入sum
  if (!node.left && !node.right) {
    sum.push(currentSum);
    return;
  }

  //呼叫自己
  getBranchSums(node.left, currentSum, sum);
  getBranchSums(node.right, currentSum, sum);
}

明日題目預告：一起來實作min-heap吧！ Ｍin-Heap construction